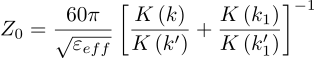Characteristic Impedance of Coplanar Waveguides with Ground

Rationale

One of the most common transmission line types that I rely on, when designing and producing homemade dual-layer PCBs, is the GCPW (Coplanar Waveguide with Ground). GCPW are similar to CPW (Coplanar Waveguide), except for the fact that it has a third return path that is a ground plane subjacent to the component side of the PCB. Like any other waveguide, the PCB substrate material, width of the central conductor and separation distance to its return paths, are the most relevant properties that define the characteristic impedance of the transmission line.

Calculating the characteristic impedance Zo of a GCPW is relatively straightforward, but difficult to do by hand, given that it relies on the Complete Eliptic Integral of the First Kind.

There are, though, approximations for the K(k) / K’(k) ratio, Hilberg[1], that make these calculations easier and faster, allowing a human to calculate Zo in an acceptable amount of time with just a hand calculator - I will cover these in a future post, as well as a faster and simpler recursive method to calculate K(k) from Miller[2].

Below, we will cover the necessary definitions and equations first, and then we’ll move into Python to help us automate the process of designing this type of waveguide.

Definitions

The figure below presents a PCB cross section for a GCPW:

Fig 1. GCPW Cross Section

The green areas in the above picture represent the PCB substrate, while the brownish areas represent the copper layers and vias.

The relative dielectric constant Er represents the PCB substrate permittivity, and for recent PCB substrates that are manufactured with FR4 material (Flame Retardant 4) we can assume typical values between 4.1 and 4.4 - but it can vary as much as from 3.8 to 4.8, depending on its operating temperature and manufacturing process.

Pay special attention on how a, b and h are represented and how they should be measured. These values, along with Er, are essential for the following equations.

Equations

The moduli k and k’ have the following mutual dependence [1]:

The value of k is the ratio of a over b, from Ghione[3]:

By the moduli mutual dependence, k’ is given by [1]:

The value of k1 is a relationship of a, b and h [3] (NOTE: There are some sources citing [3] where they incorrectly multiply h by 4, instead of by 2 - here we rely on the equation from [3] and we correctly multiply h by 2):

And by the moduli mutual dependence, k1’ is given by (NOTE: There’s a typo in [3] for this equation, where k1’ is incorrectly squared. See the moduli mutual dependence definition from [1] for proof. The equation below is already corrected):

The characteristic impedance calculation relies on the effective permittivity Eeff, that relates to Er by [3]:

Finally, the characteristic impedance Zo, is given by [3]:

Calculations

The following Python function gcpw(), accepts the input parameters a, b, h and Er and returns Zo. The example below uses mpmath, but alternatively math and scipy can be used, just by changing from where the required methods and properties are imported from:

# Author  : pah <a.t> ucodev <d.o.t> org
# Source  : https://www.ucodev.org/notes2self/characteristic-impedance-of-coplanar-waveguides-with-ground
# License : https://www.apache.org/licenses/LICENSE-2.0

from mpmath import sqrt, tanh, hyp2f1, pi

# Alternatively, scipy and math can be used
# from scipy.special import hyp2f1
# from math import sqrt, tanh, pi

def gcpw(a, b, h, Er):
    def K(k):
        # NOTE: See https://www.ucodev.org/notes2self/complete-elliptic-integral-of-the-first-kind
        return (pi / 2.) * hyp2f1(0.5, 0.5, 1., k ** 2)

    k    = a / b
    kp   = sqrt(1. - k ** 2)
    k1   = tanh((pi * a) / (2. * h)) / tanh((pi * b) / (2. * h))
    k1p  = sqrt(1. - k1 ** 2)
    Eeff = (1. + Er * ((K(kp) * K(k1)) / (K(k) * K(k1p)))) / (1. + ((K(kp) * K(k1)) / (K(k) * K(k1p))))
    Zo   = ((60. * pi) / sqrt(Eeff)) * ((K(k) / K(kp)) + (K(k1) / K(k1p))) ** -1

    return Zo

Note that K(k) here is calculated based on the hypergeometric function two-F-one as described in a previous post.

As an example, if the desired characteristic impedance of a GCPW is approximatelly 50 Ω, then:

a = 1.5 mm
b = 3.4 mm
h = 1.6 mm
Er = 4.3

Which will result in Zo = 50.09 Ω.

The units of distance used for a, b and h are irrelevant, as long as all the values are normalized to the same unit of distance.

A 3D representation of the waveguide from the example above can be seen in the image below:

Fig 2. 3D representation, with distances to scale, for a GCPW with a characteristic impedance of approximatelly 50 Ω.

The 3D representation above also shows the PCB vias connecting all the return paths togheter. The vias are spaced apart by λ / 20, that translates to approximatelly 1.5 mm for a main signal frequency of 1 GHz.

Considerations

The GCPW is an extremelly useful type of transmission line, given that when designing RF circuits, usually a ground plane is already present in most applications. So whenever a ground plane is available in the design, this type of waveguide becomes a natural choice when a transmission line is required to be designed on the component side of the PCB (i.e., in the opposite plane with regard to the ground plane).

Note that it’s advisable that both sides of the component side return path are connected togheter through the ground plane with multiple vias that extend in parallel to the waveguide, and their spacing, as a general approximation, should not exceed more than λ / 20 of the fundamental frequency. Also note that the width for both sides of the component side return paths should extend away from a more than the length of b.

Waveguides can also be used as an impedance matching circuit by using a quarter wavelength impedance matching technique, if the wavelength is short enough so a quarter of its length can be pratically acommodated in the PCB being designed.

References

[1] “From Approximations to Exact Relations for Characteristic Impedances”, Wolfgang Hilberg, published in “IEEE TRANSACTIONS ON MICROWAVE THEORY AND TECHNIQUES, VOL. MTT-17, NO. 5, MAY 1969”

[2] “Inductance formula for a single-layer circular coil”, H. C. Miller, published in “Proceedings of the IEEE (Volume: 75, Issue: 2, February 1987), Pages 256-257”

[3] “Parameters of Coplanar Waveguides with Lower Ground Plane”, G. Ghione and C. Naldi, published in “Electronic Letters, 1st September 1983, Vol 19, No. 18, Pages 734-735”

Notes

This blog post is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.

The code examples in this blog post were written by, and are copyrighted by the author of this website (www.ucodev.org), and are licensed under the Apache License, version 2.0.

If there are any questions or suggestions related to this blog post, please check the website footer for the contact information of the author.

Complete Elliptic Integral of the First Kind: K(k)

Rationale

When dealing with transmission lines, specially when designing coplanar waveguides in a PCB with specific characteristic impedances, the K(k) tend to pop in an equation or two.

Usually, when dealing with characteristic impedances in coplanar waveguides, the equations depend mostly on the K(k) / K’(k) quotient, and a few fast approximations for this division can be found in a publication by Hilberg [1]. This topic will be covered in much more detail in a future blog post.

Without fast approximations, the K(k) isn’t easy to calculate by hand, as it depends on hypergeometric functions and the intermediate calculations will rapidly grow in complexity with very large numerical values — only with the aid of a computer, it becomes feasible to solve them. So let’s dig into some definitions first before we call Python into the scene.

Definitions

The Complete Elliptic Integral of the First Kind, K(k), is defined for 0 <= k < 1, by:

As described by G. D. Anderson, et al. [2], elliptical integrals of the first and second kind can be solved with the Gaussian hypergeometric function two-F-one, defined as:

Which depends on the Rising Factorial, defined as:

Still from [2], rewritting K(k) in terms of the hypergeometric function two-F-one, yields:

And putting everything together, we have:

Calculations

Using Python to solve K(k) is extremelly straightforward if depending on scipy or mpmath isn’t an issue:

from scipy import pi
from scipy.special import hyp2f1

# Alternatively, mpmath.hyp2f1 can be used
# from mpmath import pi
# from mpmath import hyp2f1

def K(k):
    return (pi / 2.) * hyp2f1(0.5, 0.5, 1, k ** 2)

But if you need an implementation without depending on scipy nor mpmath, then a simple version, yet limited in precision, can be written as:

# Author  : pah <a.t> ucodev <d.o.t> org
# Source  : https://www.ucodev.org/notes2self/complete-elliptic-integral-of-the-first-kind
# License : https://www.apache.org/licenses/LICENSE-2.0

from functools import reduce # reduce() required to be imported in Python3

def fact(x):
    return reduce(lambda a, b: a * b, range(1, x + 1) or [1])

def fact_rising(x, n):
    return reduce(lambda a, b: a * b, [ x + i for i in range(n) or [1 - x]])

def hyp2f1(a, b, c, z):
    i = s = 0
    while True:
        _s = s + (((fact_rising(a, i) * fact_rising(b, i)) / fact_rising(c, i)) * ((z ** i) / fact(i)))

        if not (0. < (round(_s, 11) - round(s, 11)) < float('inf')): break
        s = _s
        i += 1

    return s

def K(k):
    return round(1.5707963267948966 * hyp2f1(0.5, 0.5, 1, k ** 2), 8)

The issue with the implementation above is that it will struggle to give precise results when k >= 0.92, given that there will not be enough precision in the double precision floating point variables to carry out the division of the very large rising factorial results as i increases. Although this implementation will most likely suffice for most uses, alternatively one can extend it by using numpy.float128, which will increase the precision and provide decent results up to k < 0.9911.

Considerations

All in all, if adding scipy or mpmath as a dependency is acceptable for your project, you should definetly go with it, given that creating an implementation for hypergeometric functions while not being dependent on floating point variables, will require all intermediate calculations to be performed with single digit array representations of all values, or some other technique to deal with very large, and very small, real numbers — and if not done properly, the performance of the custom implementation may end up being way worse than expected.

The addition of a solid dependency that greatly simplifies the implementation and improves the code quality and readability, should always be considered as an enhancement — unless there’s a very strong reason for not doing so.

References

[1] : “From Approximations to Exact Relations for Characteristic Impedances”, Wolfgang Hilberg, published in the “IEEE TRANSACTIONS ON MICROWAVE THEORY AND TECHNIQUES, VOL. MTT-17, NO. 5, MAY 1969”

[2] : “Hypergeometric Functions and Elliptic Integrals”, G. D. Anderson, M. K. Vamanamurthy, and M. Vuorinen, December 1992

Notes

This blog post is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.

The code examples in this blog post were written by, and are copyrighted by the author of this website (www.ucodev.org), and are licensed under the Apache License, version 2.0.

If there are any questions or suggestions related to this blog post, please check the website footer for the contact information of the author.